Definition of a horizontal asymptote: The line y = y0 is a "horizontal asymptote" of f(x) if and only if f(x) approaches y0 as x approaches + or -Concavity. Definition of a vertical asymptote: The line x = x0 is a "vertical asymptote" of f(x) if and only if f(x) approaches + or -
as x approaches x0 from the left or from the right.
Definition of a slant asymptote: the line y = ax + b is a "slant asymptote" of f(x) if and only if lim (x-->+/-) f(x) = ax + b.
Definition of a concave up curve: f(x) is "concave up" at x0 if and only ifCritical Pointsf '(x) is increasing at x0 Definition of a concave down curve: f(x) is "concave down" at x0 if and only iff '(x) is decreasing at x0
The second derivative test: If f''(x) exists at x0 and is positive, thenf ''(x) is concave up at x0. If f''(x0) exists and is negative, then f(x) is concave down at x0. Iff ''(x) does not exist or is zero, then the test fails.
Definition of a critical point: a critical point on f(x) occurs at x0 if and only if either f '(x0) is zero or the derivative doesn't exist.Extrema (Maxima and Minima)
Local (Relative) Extrema Definition of a local maxima: A function f(x) has a local maximum at x0 if and only if there exists some interval I containing x0 such that f(x0) >= f(x) for all x in I.Increasing/Decreasing Functions
Definition of a local minima: A function f(x) has a local minimum at x0 if and only if there exists some interval I containing x0 such that f(x0) <= f(x) for all x in I.
Occurrence of local extrema: All local extrema occur at critical points, but not all critical points occur at local extrema.
The first derivative test for local extrema: If f(x) is increasing (f '(x) > 0) for all x in some interval (a, x0] and f(x) is decreasing (f '(x) < 0) for all x in some interval [x0, b), then f(x) has a local maximum at x0. If f(x) is decreasing (f '(x) < 0) for all x in some interval (a, x0] and f(x) is increasing (f '(x) > 0) for all x in some interval [x0, b), then f(x) has a local minimum at x0.
The second derivative test for local extrema: Iff '(x0) = 0 andf ''(x0) > 0, then f(x) has a local minimum at x0. Iff '(x0) = 0 andf ''(x0) < 0, then f(x) has a local maximum at x0.
Absolute Extrema
Definition of absolute maxima: y0 is the "absolute maximum" of f(x) on I if and only if y0 >= f(x) for all x on I.
Definition of absolute minima: y0 is the "absolute minimum" of f(x) on I if and only if y0 <= f(x) for all x on I.
The extreme value theorem: If f(x) is continuous in a closed interval I, then f(x) has at least one absolute maximum and one absolute minimum in I.
Occurrence of absolute maxima: If f(x) is continuous in a closed interval I, then the absolute maximum of f(x) in I is the maximum value of f(x) on all local maxima and endpoints on I.
Occurrence of absolute minima: If f(x) is continuous in a closed interval I, then the absolute minimum of f(x) in I is the minimum value of f(x) on all local minima and endpoints on I.
Alternate method of finding extrema: If f(x) is continuous in a closed interval I, then the absolute extrema of f(x) in I occur at the critical points and/or at the endpoints of I.
(This is a less specific form of the above.)
Definition of an increasing function: A function f(x) is "increasing" at a point x0 if and only if there exists some interval I containing x0 such that f(x0) > f(x) for all x in I to the left of x0 and f(x0) < f(x) for all x in I to the right of x0. Definition of a decreasing function: A function f(x) is "decreasing" at a point x0 if and only if there exists some interval I containing x0 such that f(x0) < f(x) for all x in I to the left of x0 and f(x0) > f(x) for all x in I to the right of x0.Inflection Points
The first derivative test: Iff '(x0) exists and is positive, thenf '(x) is increasing at x0. Iff '(x) exists and is negative, then f(x) is decreasing at x0. Iff '(x0) does not exist or is zero, then the test tells fails.
Definition of an inflection point: An inflection point occurs on f(x) at x0 if and only if f(x) has a tangent line at x0 and there exists and interval I containing x0 such that f(x) is concave up on one side of x0 and concave down on the other side.
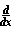
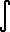
 f(t) dt = f(x)
f(t) dt = f(x) 
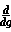 f(g) *
f(g) * 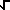 (1 - x2)
(1 - x2)