Derivatives: Min, Max, Critical Points...

Asymptotes

Definition of a horizontal asymptote: The line y = y₀ is a "horizontal asymptote" of f(x) if and only if f(x) approaches y₀ as x approaches + or - 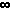. Definition of a vertical asymptote: The line x = x₀ is a "vertical asymptote" of f(x) if and only if f(x) approaches + or - 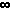as x approaches x₀ from the left or from the right.
Definition of a slant asymptote: the line y = ax + b is a "slant asymptote" of f(x) if and only if lim _(x-->+/-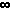) f(x) = ax + b.

Concavity

Definition of a concave up curve: f(x) is "concave up" at x₀ if and only if f '(x) is increasing at x₀ Definition of a concave down curve: f(x) is "concave down" at x₀ if and only if f '(x) is decreasing at x₀
The second derivative test: If f ''(x) exists at x₀ and is positive, then f ''(x) is concave up at x₀. If f ''(x₀) exists and is negative, then f(x) is concave down at x₀. If f ''(x) does not exist or is zero, then the test fails.

Critical Points

Definition of a critical point: a critical point on f(x) occurs at x₀ if and only if either f '(x₀) is zero or the derivative doesn't exist.

Extrema (Maxima and Minima)

Local (Relative) Extrema Definition of a local maxima: A function f(x) has a local maximum at x₀ if and only if there exists some interval I containing x₀ such that f(x₀) >= f(x) for all x in I.
Definition of a local minima: A function f(x) has a local minimum at x₀ if and only if there exists some interval I containing x₀ such that f(x₀) <= f(x) for all x in I.
Occurrence of local extrema: All local extrema occur at critical points, but not all critical points occur at local extrema.
The first derivative test for local extrema: If f(x) is increasing (f '(x) > 0) for all x in some interval (a, x₀] and f(x) is decreasing (f '(x) < 0) for all x in some interval [x₀, b), then f(x) has a local maximum at x₀. If f(x) is decreasing (f '(x) < 0) for all x in some interval (a, x₀] and f(x) is increasing (f '(x) > 0) for all x in some interval [x₀, b), then f(x) has a local minimum at x₀.
The second derivative test for local extrema: If f '(x₀) = 0 and f ''(x₀) > 0, then f(x) has a local minimum at x₀. If f '(x₀) = 0 and f ''(x₀) < 0, then f(x) has a local maximum at x₀.
Absolute Extrema
Definition of absolute maxima: y₀ is the "absolute maximum" of f(x) on I if and only if y₀ >= f(x) for all x on I.
Definition of absolute minima: y₀ is the "absolute minimum" of f(x) on I if and only if y₀ <= f(x) for all x on I.
The extreme value theorem: If f(x) is continuous in a closed interval I, then f(x) has at least one absolute maximum and one absolute minimum in I.
Occurrence of absolute maxima: If f(x) is continuous in a closed interval I, then the absolute maximum of f(x) in I is the maximum value of f(x) on all local maxima and endpoints on I.
Occurrence of absolute minima: If f(x) is continuous in a closed interval I, then the absolute minimum of f(x) in I is the minimum value of f(x) on all local minima and endpoints on I.
Alternate method of finding extrema: If f(x) is continuous in a closed interval I, then the absolute extrema of f(x) in I occur at the critical points and/or at the endpoints of I.
(This is a less specific form of the above.)

Increasing/Decreasing Functions

Definition of an increasing function: A function f(x) is "increasing" at a point x₀ if and only if there exists some interval I containing x₀ such that f(x₀) > f(x) for all x in I to the left of x₀ and f(x₀) < f(x) for all x in I to the right of x₀. Definition of a decreasing function: A function f(x) is "decreasing" at a point x₀ if and only if there exists some interval I containing x₀ such that f(x₀) < f(x) for all x in I to the left of x₀ and f(x₀) > f(x) for all x in I to the right of x₀.
The first derivative test: If f '(x₀) exists and is positive, then f '(x) is increasing at x₀. If f '(x) exists and is negative, then f(x) is decreasing at x₀. If f '(x₀) does not exist or is zero, then the test tells fails.

Inflection Points

Definition of an inflection point: An inflection point occurs on f(x) at x₀ if and only if f(x) has a tangent line at x₀ and there exists and interval I containing x₀ such that f(x) is concave up on one side of x₀ and concave down on the other side.